It is often said that science and scientists work objectively, and logic, rationalism governs science. While for the most part of the process it is true, except that the underlying axioms or beliefs dictate which thread of rationalism a particular scientist weaves through their career. This is an important question to consider, given that science thrives in communities, collaborations, and exchanges – and it becomes essentially important to acknowledge what your scientific beliefs are before finding your audience.
The foremost insights are revealed when one tries to understand how exchanges between those in physics and in mathematics happen. Physicists build a force-mass-energy intuition upon seeing something in 3D, and use mathematical language (calculus, geometry, numbers) or computational world (automaton, neural networks/LLM, bits-bytes) to describe it. Their job finishes when their first instinctive question about why this entity behaves such and such is answered. Fair. The interesting divergence from normal starts when external world is used as source of inspiration to deduce truths in mathematical/computational world. To give an example, consider the following sculpture made by my friend Binghui using flameworks. It is hard not to get tempted with an urge to encode each different colours of polyps using different numbers (integers, fractions, primes) and find an underlying law/theorem guiding the entire shape (and tweaking those theorems to build more such shapes). This is an example of churning out one particular physical observation from an external world and inferring new theorems in the mathematical world (which then could have a new physical embodiment).

Now, consider a water droplet (shaded blue) on a flat surface of the shape of a spherical cap, shown below. It would take a slight while to notice and appreciate that the toroidal gridlines (build using Riemann mapping theorem and Mobius transformation) is a mathematical universe for such droplet.
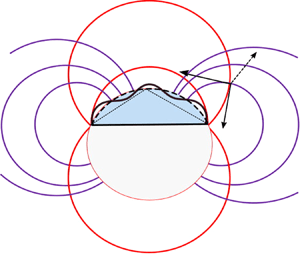
A slight more work will lead one to the fact that such lines filling up entire space do not exist if the droplet would have been elliptical in shape. This is because ellipse has two degrees of freedom, and only one can allowed to extend to infinity, while the other one has to remain fixed so that the physical constraint of the shape being drop remains as such. Again, a physical intuition/constraint is able to lend some peek into mathematical truths. What’s the underlying correspondence between physical world and mathematical truths is a mysterious question without probably any general answer. However, it is indeed a skill to deduce mathematical truths from the physical world.
Another example is that of a thin film breaking to form filaments. A slight peek into the breaking pattern unveils an underlying singularity.
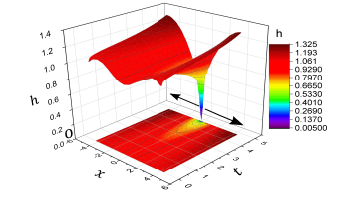
Now, what’s the nature of singularity? It is a question where scientists would differ. Physicists would treat this as physical singularity and come up with empirical or geometrical laws to model the system attaining this singularity and perform analysis for what’s after the singularity. And by all means, this is a nice way to perform and end the business. However, someone interested in inferring truths of mathematical world would ask: does this singularity exist for all kinds of perturbations to initial height of film, when one solves the equation for the thin-film to attain this singularity. This is where people focus towards studying the existence and uniqueness of solutions in PDEs. This is a very specialised and particular question, and the reason, anyone would be interested in this is because of their belief to discover hidden mathematical truths by getting motivation from physical world. Nature does provide means of finding laws or truths and is a never ending source of inspiration for mathematicians. The story does not end here.
As the business of finding mathematical theorems from cues given by the external world gets more serious, this means that the technique becomes more and more stronger. Well-developed physical theories are then used to lend new theorems to maths community, who might then make it more general and universal. Again, multitudes of beliefs idea would kick in here, because there is a difference between what you can find from seeing outside and what you can find from juggling inside (I am trying to put it as accessible as possible). There could be a plentiful of things to say here, but I would end the blog with acknowledging how Godel, Grothendieck created universes which were consistent and far from reality, and how Einstein, Witten used reality to construct a mathematical world which then was made more general and universal by others.
It is true that multitudes of beliefs create friction and disagreements between scientists; however, acknowledging that each scientist is operating with their beliefs, and coming together to construct a well-defined understanding of what we see from different viewpoints of beliefs is what we all could become good at.